Time series implementation details
These implementation details describe the stages and processing that are specific to an AutoAI time series experiment.
Implementation details
Refer to these implementation and configuration details for your time series experiment.
- Time series stages for processing an experiment.
- Time series optimizing metrics for tuning your pipelines.
- Time series algorithms for building the pipelines.
- Supported date and time formats.
Time series stages
An AutoAI time series experiment includes these stages when an experiment runs:
Stage 1: Initialization
The initialization stage processes the training data, in this sequence:
- Load the data
- Split the data set L into training data T and holdout data H
- Set the validation, timestamp column handling, and lookback window generation.
Notes:
- The training data (T) is equal to the data set (L) minus the holdout (H). When you configure the experiment, you can adjust the size of the holdout data. By default, the size of the holdout data is 20 steps.
- You can optionally specify the timestamp column.
- By default, a lookback window is generated automatically by detecting the seasonal period by using signal processing method. However, if you have an idea of an appropriate lookback window, you can specify the value directly.
Stage 2: Pipeline selection
The pipeline selection step uses an efficient method called T-Daub (Time Series Data Allocation Using Upper Bounds). The method selects pipelines by allocating more training data to the most promising pipelines, while allocating less training data to unpromising pipelines. In this way, not all pipelines see the complete set of data, and the selection process is typically faster. The following steps describe the process overview:
- All pipelines are sequentially allocated several small subsets of training data. The latest data is allocated first.
- Each pipeline is trained on every allocated subset of training data and evaluated with testing data (holdout data).
- A linear regression model is applied to each pipeline by using the data set described in the previous step.
- The accuracy score of the pipeline is projected on the entire training data set. This method results in a data set containing the accuracy and size of allocated data for each pipeline.
- The best pipeline is selected according to the projected accuracy and allotted rank 1.
- More data is allocated to the best pipeline. Then, the projected accuracy is updated for the other pipelines.
- The prior two steps are repeated until the top N pipelines are trained on all the data.
Stage 3: Model evaluation
In this step, the winning pipelines N are retrained on the entire training data set T. Further, they are evaluated with the holdout data H.
Stage 4: Final pipeline generation
In this step, the winning pipelines are retrained on the entire data set (L) and generated as the final pipelines.
As the retraining of each pipeline completes, the pipeline is posted to the leaderboard. You can select to inspect the pipeline details or save the pipeline as a model.
Stage 5: Backtest
In the final step, the winning pipelines are retrained and evaluated by using the backtest method. The following steps describe the backtest method:
- The training data length is determined based on the number of backtests, gap length, and holdout size. To learn more about these parameters, see Building a time series experiment.
- Starting from the oldest data, the experiment is trained by using the training data.
- Further, the experiment is evaluated on the first validation data set. If the gap length is non-zero, any data in the gap is skipped over.
- The training data window is advanced by increasing the holdout size and gap length to form a new training set.
- A fresh experiment is trained with this new data and evaluated with the next validation data set.
- The prior two steps are repeated for the remaining backtesting periods.
Time series optimization metrics
Accept the default metric, or choose a metric to optimize for your experiment.
| Metric | Description |
|---|---|
| Symmetric Mean Absolute Percentage Error (SMAPE) | At each fitted point, the absolute difference between actual value and predicted value is divided by half the sum of absolute actual value and predicted value. Then, the average is calculated for all such values across all the fitted points. |
| Mean Absolute Error (MAE) | Average of absolute differences between the actual values and predicted values. |
| Root Mean Squared Error (RMSE) | Square root of the mean of the squared differences between the actual values and predicted values. |
| R2 | Measure of how the model performance compares to the baseline model, or mean model. The R2 must be equal or less than 1. Negative R2 value means that the model under consideration is worse than the mean model. Zero R2 value means that the model under consideration is as good or bad as the mean model. Positive R2 value means that the model under consideration is better than the mean model. |
Reviewing the metrics for an experiment
When you view the results for a time series experiment, you see the values for metrics used to train the experiment in the pipeline leaderboard:
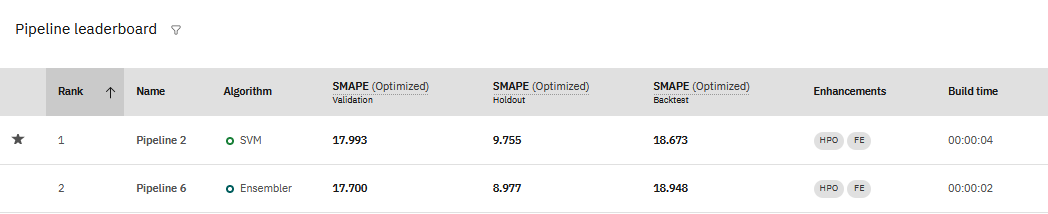
You can see that the accuracy measures for time-series experiments may vary widely, depending on the experiment data evaluated.
- Validation is the score calculated on training data.
- Holdout is the score calculated on the reserved holdout data.
- Backtest is the mean score from all backtests scores.
Time series algorithms
These algorithms are available for your time series experiment. You can use the algorithms that are selected by default, or you can configure your experiment to include or exclude specific algorithms.
| Algorithm | Description |
|---|---|
| ARIMA | Autoregressive Integrated Moving Average (ARIMA) model is a typical time series model, which can transform non-stationary data to stationary data through differencing, and then forecast the next value by using the past values, including the lagged values and lagged forecast errors |
| BATS | The BATS algorithm combines Box-Cox Transformation, ARMA residuals, Trend, and Seasonality factors to forecast future values. |
| Ensembler | Ensembler combines multiple forecast methods to overcome accuracy of simple prediction and to avoid possible overfit. |
| Holt-Winters | Uses triple exponential smoothing to forecast data points in a series, if the series is repetitive over time (seasonal). Two types of Holt-Winters models are provided: additive Holt-Winters, and multiplicative Holt-Winters |
| Random Forest | Tree-based regression model where each tree in the ensemble is built from a sample that is drawn with replacement (for example, a bootstrap sample) from the training set. |
| Support Vector Machine (SVM) | SVMs are a type of machine learning models that can be used for both regression and classification. SVMs use a hyperplane to divide the data into separate classes. |
| Linear regression | Builds a linear relationship between time series variable and the date/time or time index with residuals that follow the AR process. |
Supported date and time formats
The date/time formats supported in time series experiments are based on the definitions that are provided by dateutil.
Supported date formats are:
Common:
YYYY
YYYY-MM, YYYY/MM, or YYYYMM
YYYY-MM-DD or YYYYMMDD
mm/dd/yyyy
mm-dd-yyyy
JAN YYYY
Uncommon:
YYYY-Www or YYYYWww - ISO week (day defaults to 0)
YYYY-Www-D or YYYYWwwD - ISO week and day
Numberng for the ISO week and day values follows the same logic as datetime.date.isocalendar().
Supported time formats are:
hh
hh:mm or hhmm
hh:mm:ss or hhmmss
hh:mm:ss.ssssss (Up to 6 sub-second digits)
dd-MMM
yyyy/mm
Notes:
- Midnight can be represented as 00:00 or 24:00. The decimal separator can be either a period or a comma.
- Dates can be submitted as strings, with double quotation marks, such as "1958-01-16".
Supporting features
Supporting features, also known as exogenous features, are input features that can influence the prediction target. You can use supporting features to include additional columns from your data set to improve the prediction and increase your model’s accuracy. For example, in a time series experiment to predict prices over time, a supporting feature might be data on sales and promotions. Or, in a model that forecasts energy consumption, including daily temperature makes the forecast more accurate.
Algorithms and pipelines that use Supporting features
Only a subset of algorithms allow supporting features. For example, Holt-winters and BATS do not support the use of supporting features. Algorithms that do not support supporting features ignore your selection for supporting features when you run the experiment.
Some algorithms use supporting features for certain variations of the algorithm, but not for others. For example, you can generate two different pipelines with the Random Forest algorithm, RandomForestRegressor and ExogenousRandomForestRegressor. The ExogenousRandomForestRegressor variation provides support for supporting features, whereas RandomForestRegressor does not.
This table details whether an algorithm provides support for Supporting features in a time series experiment:
| Algorithm | Pipeline | Provide support for Supporting features |
|---|---|---|
| Random forest | RandomForestRegressor | No |
| Random forest | ExogenousRandomForestRegressor | Yes |
| SVM | SVM | No |
| SVM | ExogenousSVM | Yes |
| Ensembler | LocalizedFlattenEnsembler | Yes |
| Ensembler | DifferenceFlattenEnsembler | No |
| Ensembler | FlattenEnsembler | No |
| Ensembler | ExogenousLocalizedFlattenEnsembler | Yes |
| Ensembler | ExogenousDifferenceFlattenEnsembler | Yes |
| Ensembler | ExogenousFlattenEnsembler | Yes |
| Regression | MT2RForecaster | No |
| Regression | ExogenousMT2RForecaster | Yes |
| Holt-winters | HoltWinterAdditive | No |
| Holt-winters | HoltWinterMultiplicative | No |
| BATS | BATS | No |
| ARIMA | ARIMA | No |
| ARIMA | ARIMAX | Yes |
| ARIMA | ARIMAX_RSAR | Yes |
| ARIMA | ARIMAX_PALR | Yes |
| ARIMA | ARIMAX_RAR | Yes |
| ARIMA | ARIMAX_DMLR | Yes |
Learn more
Parent topic: Building a time series experiment